Recursion and iteration – mutual recursion and tail recursion

This is part of a series of articles about iteration and recursion.

1. Introduction to iteration
2. Introduction to recursion
3. Mutual recursion and tail recursion
4. Blurring the lines
5. Loop unrolling

I have covered the basics of recursion in a previous article. In this article I will go onto two more advanced, rare and obscure versions of recursion – mutual recursion and tail recursion.

Mutual recursion

Mutual recursion is the reason why I’m writing this series in the first place. I found myself, for the first time in a very long time, writing some mutually recursive code and thought it would be interesting to blog about. In order to describe mutual recursion, first I’ll describe normal (for want of a better word) recursion.

If you look at the fibonacci code from the previous article, the flow of what calls what looks like this:

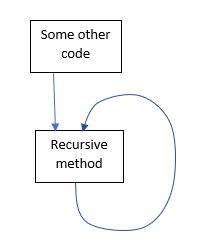
Some external method calls the recursive method. The recursive method then calls itself many times. If you look at the source code, you would see that the recursive method includes a call to itself, i.e. it’s fairly easy to spot the recursion.

Normal recursion has a tight loop involving one method. Mutual recursion has a loop that involves two or more methods, like this:

If you look at the source code for method A, there’s a call to method B. If you look at method B there’s a call to method A. Neither method has a call to itself, and so on its own neither will let you spot that there’s recursion. Execution will flow back and forth between the two methods – hopefully stopping when base conditions are reached in one or other method.

I didn’t set out to write mutually recursive code – I try to avoid it because I find it harder to get my head around when designing, and its harder to spot that its recursive. I wrote mutually recursive code because it was processing a mutually recursive data structure. It’s part of the output from a terraform tool, and looks a bit like this:

...
"root_module": {
   ...
   "resources": [
       ...
   ],
   "module_calls": {
      "accounts-database": {
         ...
         "module": {
            ...
            "resources": [
               ...
            ],
            "module_calls": {
               "sql-server": {
                   ...
                   "module": {
                      ...
                  }
               },
               ...
            }
         }
      },
      ...
   }
}

A module (the root module starting on line 2, the accounts database module starting on line 10, the sql server module starting on line 16 etc.) can contain 0 or more module calls, which in turn can contain modules etc. So I defined a method to process a module, a method to process a module call, and they called each other in a mutually recursive way.

Tail recursion

Tail recursion is a way to structure the flow of things in a non-mutually recursive method, so that once the recursive call returns there’s no further work to do and so the calling instance can also immediately return. This probably isn’t immediately clear, so I’ll explain it a bit with the aid of the factorial function.

The factorial function f(n) is defined as:

1. f(0) = 1
2. f(n) = n * f(n-1)

which means that e.g. f(7) = 7 * 6 * … * 2 * 1. It’s also written as e.g. 7!.

The simplest, non-tail-recursive, way to write this is like this:

int factorial(int n)
{
   if (n == 0) { return 1; }

   return n * factorial(n-1);
}

If you look at the work that’s done for e.g. factorial(4), it could be represented like this. As with the fibonacci example in the previous article, I’m putting in square brackets to show what goes with what.

1. factorial(4) = 4 * factorial(3)
2. factorial(4) = 4 * [3 * factorial(2)]
3. factorial(4) = 4 * [3 * [2 * factorial(1)]]
4. factorial(4) = 4 * [3 * [2 * [1 * factorial(0)]]]
5. factorial(4) = 4 * [3 * [2 * [1 * 1]]]
6. factorial(4) = 4 * [3 * [2 * 1]]
7. factorial(4) = 4 * [3 * 2]
8. factorial(4) = 4 * 6
9. factorial(4) = 24

The key thing to note here is that there’s stuff between one layer of square brackets and the next – the square brackets aren’t next to each other like this: [[. When the inner call returns, there’s work that has to happen with its result before the bigger result can be passed on. Or, putting it a slightly different way, the work that links one layer’s calculations with the next is done after the lower layer has been returned. With tail recursion we will change it so that this work is done as the lower layer is being called, so that none remains to be done once it has returned. This needs a little bit of a re-write, like this:

int factorial(int n, int accumulator)
{
   if (n == 0) {return accumulator;}

   return factorial(n-1, n * accumulator);
}

// example of it being called
int myResult = factorial(4, 1);

If your language permits it, you could simplify the calling of the method by using a default value for accumulator (defaulting it to 1), so you could do e.g. factorial(4) again. I’ll go through 4! again, using this version of the code:

1. factorial(4, 1) = [factorial(3, 4)]
2. factorial(4, 1) = [[factorial(2, 12)]]
3. factorial(4, 1) = [[[factorial(1, 24)]]]
4. factorial(4, 1) = [[[[factorial(0, 24)]]]
5. factorial(4, 1) = [[[24]]]
6. factorial(4, 1) = [[24]]
7. factorial(4, 1) = [24]
8. factorial(4, 1) = 24

You’ll notice that there’s nothing between one square bracket and the next. You can also see that the work to link one layer’s calculations to the next is done as the lower layer is called (the n * accumulator part), rather than after the lower layer has returned. These are two ways of saying the same thing.

Why you would want to do tail recursion is something I’ll explain in the next article.

Summary

There are a few slightly different flavours of recursion – including the normal kind from the previous article, mutual recursion, and tail recursion. Most of the time when I use recursion it’s the normal kind, but it’s worth knowing that the other two exist.