Despite its scarily maths-sounding name, I suspect that you have already come across modulo arithmetic, even though it probably didn’t have that name. In this article I’ll go into a few examples of modulo arithmetic in the everyday world, and how the practical limitations faced by computers cause modulo arithmetic to crop up when you don’t expect it (and how this can be a problem).
Number line vs. number circle
You have probably been shown the idea of numbers being in a line, stretching from minus infinity on the left to plus infinity on the right. If you ignore exotic things like complex numbers, there are two interesting properties of this line:
- All numbers are somewhere on this line
- If you start at any number and repeatedly add (or subtract) some other number (e.g. 1), each time you do the addition or subtraction you will get to a number you haven’t seen before: 17 becomes 18, 19, 20 etc. forever

I hope that this is something you’ve come across before, even if you don’t necessarily think about it all the time. It’s behind the normal arithmetic that you do every day.
The alternative – modulo arithmetic – requires a different model for numbers. Instead of an infinitely big collection of values stretched out along a line, there’s a finite collection of values arranged around a circle:
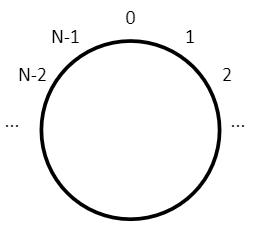
For simplicity, let’s assume our circle has the numbers 0-6:

If we start at 0 and add 1 a few times we will get the values 0, 1, 2, 3, 4, 5, 6. What happens if we add 1 again? We do what we have already done – move one place around the circle. It’s just that this time we get to 0 again. As we continue adding 1 we will continue to 1, 2, 3, 4 etc. Similarly, if we start at 4 and repeatedly subtract 1, we will get the values 4, 3, 2, 1, 0, 6, 5 etc.
This is modulo arithmetic to base 7 – the modulo bit says we’re using a number circle rather than a number line, and the base 7 bit says our number circle has 7 different values on it ranging 0-6.
This might seem like an unnecessarily limited and useless bit of maths, so I’ll now explain how you’ve probably been doing modulo arithmetic to various bases without realising it.
Rhythms in time
The choice of 7 values in the previous example wasn’t a coincidence. If I swap the values 0-6 for some others, this will probably be more familiar:

We’re used to there only being 7 different days of the week. If we start at Wednesday, repeatedly going forwards in time by a day gives Thursday, Friday, Saturday, Sunday, Monday, Tuesday, Wednesday… Even though it’s not numbers, this is still modulo arithmetic to base 7.
Within a day we have another level of modulo arithmetic, to base 24 (normally laid out a bit better than this):

There is also a pair of 12-value circles we could use (the 12 hours a.m. and the 12 p.m. ones) but these don’t fit so neatly with this article because they’re traditionally labelled 1-12 rather than 0-23.
Above the level of the day we have another level of modulo arithmetic, to base 12:

There’s another level here too:
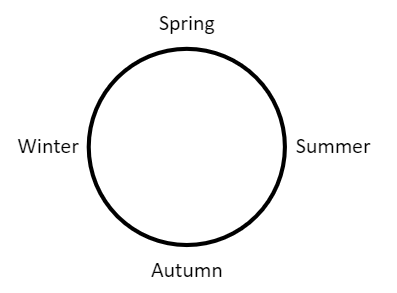
It’s not a complete surprise that these patterns are all modulo arithmetic, i.e. rely on values on a circle rather than a line. This is because behind the scenes there are important physical circles* – the Earth rotating on its axis, the Earth orbiting the Sun etc.
*None of these is a perfect circle, but they are close enough. The Earth is an oblate spheroid, and Kepler says that orbits of planets, moons etc. are ellipses rather than circles. What I find interesting is that some of these patterns are purely physical, but others are the result of choices made by humans. For instance, the repeating pattern of seasons depends on the tilt of the Earth’s axis, its orbit around the Sun, and where you are on the surface of the Earth, but the division of a day into 24 hours is an arbitrary choice (why not 17 or 59?). Similarly, the division of the year into academic terms or semesters is a fairly arbitrary human choice.
These patterns don’t always line up – months don’t always start on the same day of the week as each other, or from one year to the next. This reminds me of polyrhythm and other similar effects in music, such as in Weird Fishes by Radiohead.
Music
Another example of modulo arithmetic is music. Music pitches are represented by the letters A-G (with occasional sharp or flat signs). There are twelve different values, so starting at A and then going up in semi-tones continues until you get to G#, and then it’s back to A again.
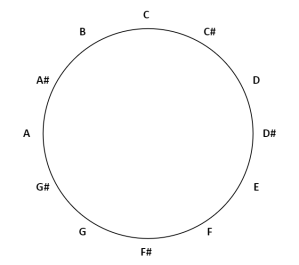
When notes are in a circle like this, they’re often not presented in this order. If you go up 7 semi-tones (7 values), that is also known as going up a fifth:

You can go up a fifth again, which because it’s the equivalent of 14 values up from the original value and there are only 12 different values, means we have to loop around through the start again. If you keep doing this, eventually you get back to the note you started on:

If, instead of showing this as the values in the normal order with lines that cross over, you reorder the values to show them in the order you visit them as you follow the lines of this star, you get this order:
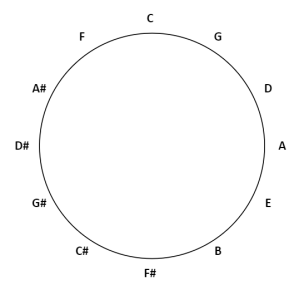
This is known as the circle of fifths.
Sneaky modulo arithmetic in programming and cars
Programmers do modulo arithmetic, sometimes without realising that they are, due to real world limitations of computers. It also shows up in cars.
When you store a number in a computer, it’s tempting to think that this number is on the number line as you’re used to. However, the space allocated to store this number is finite, which means that only a finite number of values is possible. Due to the binary nature of the underlying stuff, the number of values is often related to a power of 2. 8 bits’ worth of space means 256 possible values, 16 bits means 65,536 possible values etc.
If you start at 0, and repeatedly add 1 to a value stored in 8 bits, things are fine all the way to 255. If you add 1 again, it loops around back to 0. This is known as overflow. If you repeatedly subtract 1 from a value, then it loops around from 0 to 255, which is underflow. (Note that this limitation where you can’t store all the values you might want to is the simpler form of this kind of problem. If you try to store floating point numbers, which are the computer equivalent of scientific notation such as 6.022 x 1023, then you have extra problems.)
Overflow is what happened with the Y2K problem. Numbers were stored in decimal rather than binary, and only 2 digits were allocated. This would mean that repeatedly adding a year to e.g. 86 (which was interpreted as 1986) was fine up to 1999. However, after that it would overflow to 00, which was interpreted as 1900 rather than 2000. Time would appear to jump backwards, which could violate all kinds of assumptions that kept code working.
Overflow is the same thing that unscruplous car sellers use, to make a car appear to have travelled fewer miles than it really had, but it goes by the name car clocking. An odometer has only a fixed number of digits, e.g. 6, but is fixed to only ever allowed the number of digits to increase (even if you drive in reverse). If a car has done 50,000 miles and you connect the odometer up to something like a drill so you can rapidly add more and more miles, you can add on 950,002 miles and it will overflow to only 2 miles.
Spirals rather than circles
So far I have described things like musical notes, days of the week etc. as lying on a circle. This is certainly true, but isn’t the full picture. If you start at the lowest A note on a piano and move 12 semi-tones to the right, you definitely end up on A again. However, it’s A in the next octave up. Similarly if you start on a Monday and move on 7 days, you definitely end up on Monday again. However, it’s Monday of the following week.
One way to combine things staying the same (A becomes A again) and things being different (one octave to the next one) is to think of the values as being laid out on a spiral rather than a circle. If you look at the spiral end-on, as you go from the lowest A to the A of the next octave up, you appear to end where you started (on A) as the two As sit one in front of the other on the spiral. However, if you look at the spiral from the side, you see the note is continuously moving from one end to the other.
Another way of thinking about it is to think of how numbers are represented in normal Arabic numbers. The right-most digit only ever goes 0 to 9. If you start at 0 and keep adding 1, once the number has got to 9, then the right-most digit goes back to 0 again. This is like modulo arithmetic. However, the column to the left goes up from 0 (which is normally hidden) to 1 so the full thing is 10. You can think of a musical note as being e.g. 3C or 7F, where the right-most digit is normal name for the note and the left-most is which octave it’s in. (Normally notes would be written C3 or F7, which is the reverse order of how we’d write numbers such as 10, also known as little endian rather than big endian.)
Conclusion
There’s no great point to this article, other than to point out how modulo arithmetic crops up a lot even if it doesn’t go by that name. Many everyday things, such as days of the week or musical notes, are a form of modulo arithmetic. Computer programmers can get bitten by the modulo arithmetic imposed on them by real world computers, leading to overflow and underflow.